Lambda calculus我们一般称为λ演算，最早是由邱奇（Alonzo Church，图灵的博导）在20世纪30年代引入，当时的背景是解决函数可计算的本质性问题，初期λ演算成功的解决了在可计算理论中的判定性问题，后来根据Church–Turing thesis，证明了λ演算与图灵机是等价的。
好了，经过上边简单的介绍，大家应该对λ演算有了初步印象。下面我将重点介绍λ演算的具体内容，并且阐述λ演算是如何奠基了我们现在常用的编程语言（如：Java、python、Lisp等）。
λ演算的语法与求值
语法(syntax)
因为λ演算研究的是函数的本质性问题，所以形式极其简单：
E = x variables
| λx. E function creation(abstraction)
| E1 E2 function application
上面的E称为λ-表达式(expressions)或λ-terms，它的值有三种形式：
- 变量(variables)。
- 函数声明或抽象(function creation/abstraction)。需要注意是的，函数中有且仅有一个参数。在λx. E中，x是参数，E是函数体
- 函数应用(function application)。也就是我们理解的函数调用，但官方术语就叫函数应用，本文后面也会采用“应用”的叫法。
λ表达式例子
上面就是λ演算的语法了，很是简单吧。下面看几个例子：
- 恒等函数
λx.x - 一个返回恒等函数的函数
λy. (λx.x)可以看到，这里的y参数直接被忽略了
在使用λ演算时，有一些惯例需要说一下：
- 函数声明时，函数体尽可能的向右扩展。什么意思呢，举个例子大家就明白了
λx.x λy.x y z 应该理解为 λ x. (x (λy. ((x y) z)))
- 函数应用时，遵循左结合。在举个例子： x y z 应该解释为 (x y) z
Currying带有多个参数的函数
从上面我们知道，λ演算中函数只有一个参数，那两个参数的函数的是不是就没法表示了呢，那λ演算的功能也太弱了吧，这就是λ的神奇之处，函数在本质上只需要一个参数即可。如果想要声明多个参数的函数，通过currying技术即可。下面来说说currying。
λx y. (+ x y)---->λx. (λ y. + x y)
上面这个转化就叫currying，它展示了，我们如何实现加法（这里假设+这个符号已经具有相加的功能，后面我们会讲到如何用λ表达式来实现这个+的功能）。
其实就是我们现在意义上的闭包——你调用一个函数，这个函数返回另一个函数，返回的函数中存储保留了调用函数的变量。currying是闭包的鼻祖。
如果用Python来表示就是这样的东西：
def add(x):
return lambda y: x+y
add(4)(3) //return 7
如果用函数式语言clojure来表示就是：
(defn add [x]
(fn [y] (+ x y)))
((add 4) 3) ;return 7
求值(evaluation)
在λ演算中，有两条求值规则：
- Alpha equivalence( or conversion )
- Beta reduction
Alpha equivalence
这个比较简单也好理解，就是说λx.x与λy.y是等价的，并不因为换了变量名而改变函数的意义。
简单并不说这个规则不重要，在一些变量覆盖的场合很重要，如下这个例子：
λx. x (λx. x)如果你这么写的话，第二个函数定义中的x与第一个函数定义中的x重复了，也就是在第二个函数里把第一个的x给覆盖了。
如果改为λx. x (λy. y)就不会有歧义了。
Beta reduction
这个规则是λ演算中函数应用的重点了。一句话来解释就是，把参数应用到函数体中。举一个例子：
有这么一个函数应用(λx.x)(λy.y)，在这里把(λy.y)带入前面函数的x中，就能得到最终的结果(λy.y)，这里传入一个函数，然后又返回一个函数，这就是最终的结果。
求值顺序
考虑下面这个函数应用
(λ y. (λ x. x) y) E
有两种计算方法，如下图
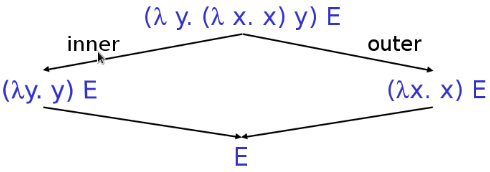可以先计算内层的函数调用再计算外层的函数调用，反之也可。
根据Church–Rosser定理，这两种方法是等价的，最终会得到相等的结果，如上图最后都得到了E。
但如果我们要自己实现一种语言，就有可能必选二选其一，于是有了下面两种方式：
- Call by Value(Eager Evaluation及早求值) 也就是上图中的inner，这种方式在函数应用前，就计算函数参数的值。如：
(λy. (λx. x) y) ((λu. u) (λv. v)) --->
(λy. (λx. x) y) (λv. v) --->
(λx. x) (λv. v) --->
λv. v
- Call by Name (Lazy Evaluation惰性求值) 也就是上图中的outer，这种方式在函数应用前，不计算函数参数的值，直到需要时才求值。如：
(λy. (λx. x) y) ((λu. u) (λv. v)) --->
(λx. x) ((λu. u) (λv. v)) --->
(λu. u) (λv. v) --->
λv. v
值得一提的是，Call by Name这种方式在我们目前的语言中，只有函数式语言支持。
λ演算与编程语言的关系
在λ演算中只有函数（变量依附于函数而有意义），如果要用纯λ演算来实现一门编程语言的话，我们还需要一些数据类型，比如boolean、number、list等，那怎么办呢？
λ的强大又再一次展现出来，所有的数据类型都能用函数模拟出来，秘诀就是
不要去关心数据的值是什么，重点是我们能对这个值做什么操作，然后我们用合法的λ表达式把这些操作表示出来即可。
听上去很些云里雾里，但看了我下面的讲解以后，你会发现，编程语言原来还可以这么玩，希望我能把这部分讲清楚些，个人感觉这些东西太funny了 :-)
好了，我们先从最简单——boolean的开始。
编码Boolean
Ask：我们能对boolean值做什么？ Answer：我们能够进行条件判断，二选其一。
好，知道了能对boolean的操作，下面就用λ表达式来定义它：
true = λx. λy. x
false = λx. λy. y
if E1 then E2 else E3 = E1 E2 E3
来简单解释一下，boolean就是这么一个函数，它有两个参数（通过currying实现），返回其中一个。下面看个例子：
if true then u else v 可以写成
(λx. λy. x) u v ---> (λy. u) v ---> u
哈哈，很神奇吧，更精彩的还在后头呢，继续
编码pair
这里简单解释下pair，其实就是序列对，如(1 2)、(hello world)，这些就是pair，只有两个元素，但不要小看了pair，我们用的list就是通过pair连接起来形成的。
Ask：我们能对pair做什么？ Answer：我们能够选择pair中的任意一个元素
好，知道了能对pair的操作，下面就用λ表达式来定义它：
mkpair x y = λb. (b x y)
fst p = p true
snd p = p false
这里用到了true与false的编码。解释一下： pair就是这么一个函数，参数是一个boolean值，根据这个参数确定返回值。还是看例子：
fst (mkpair x y)--->(mkpair x y) true--->true x y--->x
这样我们就能取到pair的第一个元素了。很好玩吧，下面的更有趣，继续
编码number
这里讲的number是指的自然数。
Ask：我们能对number做什么？ Answer：我们能够依次遍历这些数字
好，知道了能对number的操作，下面就用λ表达式来定义它：
0 = λf. λs. s
1 = λf. λs. f s
2 = λf. λs. f (f s)
......
解释一下，利用currying，我们知道上面的定义其实相当于一个具有两个参数的函数：一个函数f，另一个是起始值s，然后不断应用f实现遍历数字的操作。先不要管为什么这么定义，看了下面我们如何定义加法乘法的例子你应该就会豁然开朗了： 首先我们需要定义一个后继函数(The successor function)
succ n = λf. λs. f (n f s)
然后，就可以定义加法与乘法了
add n1 n2 = n1 succ n2
mult n1 n2 = n1 (add n2) 0
只看定义要想弄懂应该还是有些困难，下面看个具体的例子：
add 0 = (λn1. λn2. n1 succ n2) 0 // 这里直接根据上面 add 定义进行展开
-------将 0 带入 n1，可得-------->
λn2. 0 succ n2 = λn2. (λf. λs. s) succ n2
-------将 succ 带入 f，n2 带入 s，可得-->
λn2. n2 = λx. x
我第一次看这个例子有个疑问，add不是两个参数吗，你怎么就加一个0呢？其实还是currying没理解好，两个参数的函数内部不也是用一个参数的函数来表示的嘛，如果只传递一个参数，那么我们就知道还会返回一个函数，本例中就是λx. x，这是恒等函数，也就是说加 0 ,相当于什么也没加，还是本身。
哈哈，看来也不过如此嘛，如果你能看到这里，说明你已经对lambda掌握的差不多了。下面再来看个“难点”的例子——1+1：
add 1 1 --->
1 succ 1 --->
succ 1 --->
λf. λs. f (f s) ---> 2
最后一个例子，2*2：
mult 2 2 --->
2 (add 2) 0 --->
(add 2) ((add 2) 0) --->
2 succ (add 2 0) --->
2 succ (2 succ 0) --->
succ (succ (succ (succ 0))) --->
succ (succ (succ (λf. λs. f (0 f s)))) --->
succ (succ (succ (λf. λs. f s))) --->
succ (succ (λg. λy. g ((λf. λs. f s) g y)))
succ (succ (λg. λy. g (g y))) --->......---> λg. λy. g (g (g (g y))) = 4
不要一看到这么多步骤就吓跑了，原则很简单，就是不断进行函数应用，需要注意的就是这里的2、0不再是单纯的数字了，它是从具有两个参数的函数，如果你应用时只传入一个参数，说明它还会返回一个函数。
不管怎样，如果你已经看到了这里，我希望你能把上面这个乘法的例子看懂，就是不断进行函数应用而已，没什么东西，我觉得难点在于思维的转化，因为以前都很理所当然认为2×2=4了，而不知道这么简单的计算后面的本质性东西，通过这个例子，希望大家能明确一点：值是什么不重要，重要的是我们能对这个值进行的操作。
最后再来一个收尾菜：
如果想要判断一个数字是否为0，可以这么定义
iszero n = n (λb. false) true
λ-演算与图灵机
本文一开始就说明了，λ-演算与图灵机是等价，这里简单说下我对图灵机的理解：
在一个不限时间、不限资源的前提下，图灵机通过前进、后退、跳转、输出1或0这四个简单的命令，在一条无限长的纸带上执行事先编好的程序。
根据目前的证明，图灵机是宇宙间最强大的机器（理想中的），我们现有的计算机都没有超过图灵机。
如果说一个语言是图灵完备的，就是说，世界上任何可计算性问题，它都能解决。
我们现有的命令式语言，如C、Java等就是以图灵机为基础的。如果说这些语言图灵完备，需要具有以下两个特征：
- 有if、goto语句（或while、for之类的循环语句）
- 能够进行赋值操作（也就是改变内存状态）
与图灵机对应，λ-演算的直接影响是函数式编程语言，如lisp、Haskell等，如果说这些函数式语言图灵完备，需要有以下两个特征：
- 能够进行函数抽象（也就是函数定义）
- 能够进行函数应用（也就是函数调用）
鉴别一个语言是不是函数式的标准是：这个语言能否在运行时创建函数，如果能，就是函数式语言。
总结
通过上面长篇大论（希望你能抽时间看完），我们用一些无意义符号表达了我们已经熟知的一些概念，这就是λ演算的精髓之处，通过一套形式化的规则来描述这些东西，要知道，这里面的很多东西我们现如今想当然的接受了，但如何让笨重的计算机来理解这个世界呢，这就需要这些形式化的规则来指导了。
我这里介绍的lambda calculus并不完全，只是其中的一部分，像递归这个重要的东西就没说，大家凭借兴趣再自己去看吧，我觉得我这篇文章就是个砖头，希望能引出大家的宝玉就好。
我们现在的编程语言趋向于多范式化，像python、ruby的兴起就说明了这点。 因为纯函数式语言不能改变变量状态，这个恐怕在很多场合不适用吧。 纯OO也不好，因为我们大多数程序员，都是用OO的语言来写过程式的程序，看看大家有多Helper类，Util类就明白了。
有了对 lambda 的认识后，就可以尝试下一个主题了——Y 算子，下面给出我觉得讲解的最好的一篇文章：
最后，推荐王垠的一篇文章，以飨读者：