计算思维之三语义符号化表达与计算

##0和1与逻辑——思维符号化表达与逻辑运算

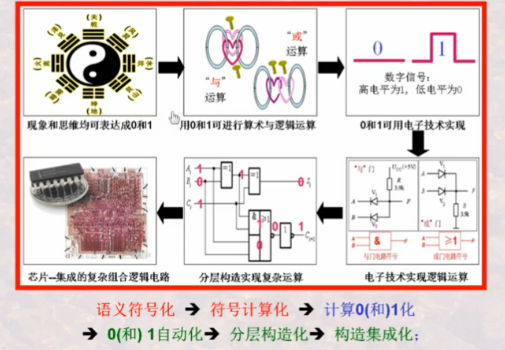
有上图可知，在进行语义符号化表达与计算过程中分为如图所示的六步，下面分别进行阐述。

1. 语义符号化与符号计算化

1.1 自然现象

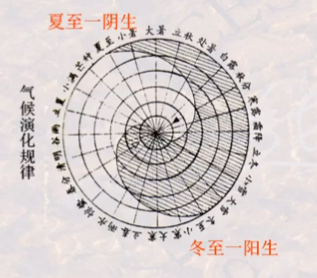
老师用的例子是我们中国的经典著作《易经》讲述的，首先讲解卦相，最基本的两类元素是“阴”与“阳”，有这两种元素的不同组合，可以得到更多的卦相;此外，我们还可以对“阴”与“阳”进行语义化，比如“阴”代表“凉”，“阳”代表“热”，这样我们就可以得到二十四节气的变化图。

1.2 思维符号化与逻辑运算

逻辑是指事物因果之间所遵循的规律，是现实中普适的思维方式。

逻辑的基本表示形式是命题与推理，推理即根据由简单命题的判断推导得出复杂命题的判断结论的过程。命题由语句表述，即内容为“真”或为“假”的一个判断语句！

举个例子：在一次中学测验过程中，有三位老师做了测评：A.学习委员及格;B.有人不及格;C.全班都不及格。在考试后，证明只有一个老师的预测是对的，请问谁对谁错？

求解过程：

命题A：“学习委员及格（有人及格）”
命题B：“有人不及格”
命题C：“全班都不及格”

由题目假设和命题之间的关系得出“已知”：A、B、C只有一个为真

如果A真，则C假;如果C真，则A假
如果B真，而A，C可能有一个为真，与题目矛盾，所以B为假。
如果B假，则“全班都及格”为真，而由此推断C为假。

由上“已知”，推理：A为真。

如果我们将逻辑表达为0和1及其运算：1为真，0为假，运算规则有“AND”、“OR”、“NOT”、“XOR”。

一个命题用A、B等符号表达，其中符号的值可能为0也可能为1

求解过程：

命题A：“学习委员及格（有人及格）”
命题B：“有人不及格”
命题C：“全班都不及格”

已知：

( A AND (NOT C) ) OR ( (NOT A) AND C ) = 1
(NOT B) AND ( ( A AND (NOT C) ) OR ( (NOT A) AND C ) ) = 1
(NOT B) AND (NOT C) = 1

组合形成所有可能解：

{<A=1,B=0,C=0>,<A=0,B=1,C=0>,<A=0,B=0,C=1>}

就上面这三种情况，将这三种情况分别带入到已知条件中，都满足的便是问题的解：

<A=1,B=0,C=0>

####深入知识：

亚里士多德（公元前384-322），古希腊哲学家：形式逻辑

典型概念：命题、推理、三段论

莱布尼茨（1646-1716），德国数学家：数理逻辑

典型概念：谓词、谓词演算

布尔（1815-1864），德国数学家：布尔代数

典型概念：布尔量、布尔值、布尔运算、布尔操作

其他：时序逻辑（Temporal Logics）、模态逻辑（Model Logics）、归纳逻辑（Inductive Logics）、模糊逻辑（Fuzzy Logics）、粗糙逻辑（Rough Logics）、非单逻辑等

整个第一大节所说为语义符号化表达与计算过程的前两步的内容。

2. 计算0/1化

这一部分主要是数值与非数值的数字化表示。

2.1 数值信息的表示

数值信息比较好表示，无非就是原码、反码、补码这些东西，其中我有疑问的是为什么使用补码后就可以在进行算数运算时把符号位也算进去？？

//举个例子，用5位二进制为表示数字，其中一位为符号位，计算10-3=？, -5-7=?
    0 1010            1 1011
+)  1 1101         +) 1 1001
------------    ------------
    0 0111            1 0100
    这是7的反码        这是-12的反码

经过一番google后发现了其中的奥秘，因为现在计算机中只有加法器，没有减法器（这里我还不知道为什么计算机设计时没什么没有减法器，不知道是出于什么考虑），所以计算机需要把所有的运算（包括减法，乘法，除法）转化为加法运算，补码就是为了将减法运行转化为加法运算而提出的概念。补码的本质就求模运算，可以这么想，以我们常见的分钟（模为60）为例，假设现在是30分，要想回到20分，有两种途径：

在30分的基础上，减去10分钟，30-10=20
在30分的基础上，加上50分钟，如果不考虑小时的大小，那么30+50-60=20,也是回到了20分

我们都知道负数的补码=反码+1，现在有了模的概念，我们还有这么个公式，补码=模-|负数|。

上面时间的例子，要想得到-10分钟的补码，我们用60-10即可得到补码50,在用模的思想来考虑补码时，就没有什么符号位的概念了，符号位和其他数码位一样，就是通过模减去负数的绝对值得到的，最高位该是0就是0，该是1就是1，比如为什么-128的补码是1000 0000呢，因为

//用模的概念来求反码
    1 0000 0000
-)    1000 0000
-----------------
      1000 0000

从上面可以看出，模就是现有二进制能表示的范围（在8位二进制中，表示范围为0～255,即256个不同的元素）。如果进一步推导可以得到1 0000 0000 = 1111 1111 + 1，那么求-128的补码的过程还可以这么做：

//补码=反码+1 的本质
      1111 1111
-)    1000 0000
-----------------
      0111 1111
+)    0000 0001
-----------------
      1000 0000

这样求负数补码的过程就对应了：

先求一个负数的反码（减法过程）
反码+1（加1过程）

当然，模的概念是我们人为的理解，计算机肯定不会这么“理解”，它是严格按照补码=反码+1的公式来运作的，因为采用模的思路来计算补码时需要用到减法，而计算机是不会做减法的。

图2. 8位二进制的补码表

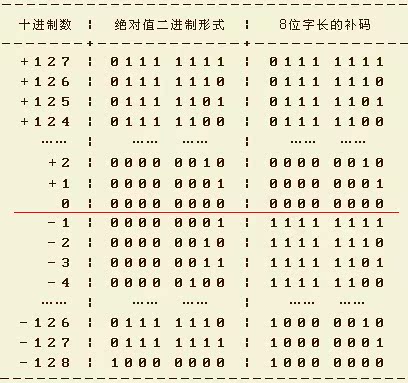
如图2所示，8位二进制的补码表示的数值范围在-128～+127之间，之所以负数比正数的绝对值大1是因为只有+0,没有-0,在补码=反码+1公式中的+1操作把-0加没了，而与之对应的是负数的另一端向前（向负数轴方向）加1不就得到了-128了嘛。

2.2 非数值信息的表示

这里无非就是各种编码，像ASCII，BCD码,Unicode编码。这里不同的编码所用的字节长度是不一样，所以我们在声明变量是需要指定变量的类型。

汉字内码，汉字在计算机内部采用汉字内码编码，汉字内码是一两字节且最高位均为1的编码
汉字输入码，是用键盘上的字母符号编码每一个汉字的编码，常见的有：拼音码、字型码、区位码……
汉字字型码，用0和1编码无亮点和有亮点像素，形成汉字字型的一种编码。

3. 自动化0/1，分层构造化，构造集成化

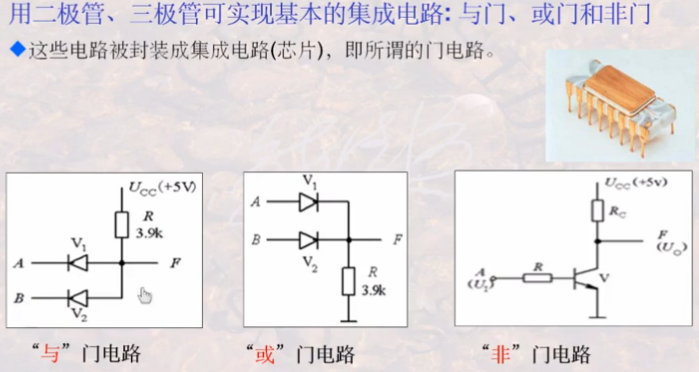
实现0和1的基本元器件：电信号和继电器开关、二极管、三极管。话说这一部门主要是数字逻辑部分的知识。这让我想起了我大学的沙老师。下面给几张电路图找找感觉：用二极管实现门电路

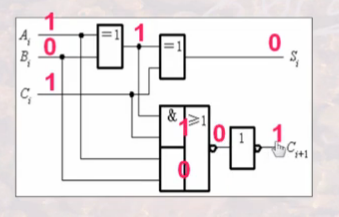
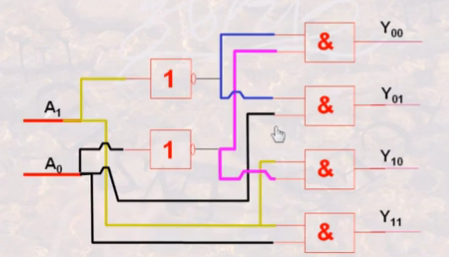
复杂的逻辑器件是通过已证明无误的简单器件构成。这体现了分层处理问题的思想，和计算机网络上的ISO/OSI七层协议一样。

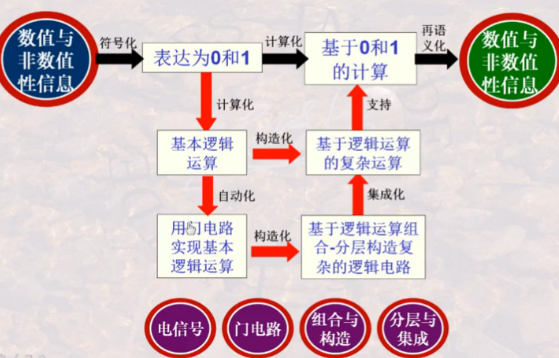最后这张图片是这部分的一个总结。