到今天为止终于把第二章看完了,相比于第一章,感觉难点少了些,这章主要是通过大量例子(主要有图形语言、区间运算、符号求导、集合的表示、通用型算术运算)来熟悉构造数据抽象的相关技能。下面来回顾总结一下第二章。
数据抽象的意义
在第一章中,只是进行了一些数值演算,这是比较简单的数据,并没有体现出数据抽象的意义,本章一开始就通过有理数的运算这个例子引出了数据抽象的意义。 数据抽象的基本思想,就是设法构造出一些使用复合数据对象的程序,使它们可以像操作数值等简单数据类型一样操作“抽象数据”。通过构造复合数据(与构造复合过程类似)可以达到下面的效果:
- 降低程序间的耦合度
- 提高设计的模块性
- 增强语言表达能力,为处理计算问题提供更多手段和方法。
第二章主要围绕下面两个部分展开:
- 如何构造复合数据对象(通过数据组合)
- 如何处理复合数据对象
其他一些细节点还包括:
- 复合数据如何支持以“匹配和组合”方式工作的编程接口
- 通过定义数据抽象,进一步模糊“过程”和“数据”的差异
- 符号表达式的处理,这种表达式的基本部分是符号而不是数 通用型(泛型)操作,使同样操作可能用于不同的数据
- 数据制导(导向/驱动)的程序设计,方便新数据类的加入
过程抽象与数据抽象
一个过程描述了一类计算的模式,又可以作为元素用于实现其他(更复 杂的)过程。因此过程是一种抽象——过程抽象。过程抽象的优势在于:
- 屏蔽计算的实现细节,可以用任何功能/使用形式合适的过程取代
- 规定了使用方式,使用方只依赖于抽象的使用方式约定
数据抽象的情况类似。 一个数据抽象实现一类数据所需的所有功能,又像基本数据元素一样可以作为其他数据抽象的元素。主要优势:
- 屏蔽一种复合数据的实现细节
- 提供一套抽象操作,使用组合数据的就像是使用基本数据
- 数据抽象的接口(界面)包括两类操作:构造函数和选择函数。构造函数基于一些参数构造这类数据,选择函数提取其内容
后面将说明(在第三章😊),如果需要支持基于状态的程序设计,那么就需要增加另外 一类变动操作(mutation,修改操作)。
数据抽象的语言支持
一般来说,实现数据抽象,编程语言需要提供下面三种机:
- 粘合机制,支持把一组数据对象组合成一个整体(通过闭包实现)
- 操作定义机制,定义针对组合数据的操作(通过scheme内置的define实现)
- 抽象机制,屏蔽实现细节,使组合数据能像简单数据一样使用(通过数据导向的程序设计风格实现)
处理复合数据的一个关键概念是闭包,这里的闭包概念来自抽象代数,指的是
通过数据对象组合起来得到的结果,还可以通过同样的操作再进行再次组合。
这个概念和我们在JavaScript等现代编程语言中的概念(一种为表示带有自由变量的过程而用的实现技术)不一样,要注意区分。
序对pair
Scheme的基本复合结构称为“序对”,序对本身也是数据对象,可以用于构造更复杂的数据对象(也就是表,list)。例如
(define x (cons 3 4))
(define y (cons 5 6))
(define z (cons x y))
; 注意理解序对pair 与表list 的区别
(define x (cons 1 2))
(define y (list 1 2))
(cdr x) ; 2
(cdr y) ; (2)
常规过程性语言都没有内部的表数据类型,但是我们在算法与数据结构课上,一般都用C语言实现过各种表(单向双向链表,环形链表等)结构,C++的标准STL库的list,Java集合框架中的List。
表及其相关概念是从 Lisp 开始开发,现已经成为很多技术的基础:
- 动态存储管理已经成为日常编程工作的基本支持
- 链表的定义和使用是常用技术(想想Java 中你用了多少次ArrayList吧)
- 有关表的使用和操作,以及各种操作的设计和实现,都可以从Lisp的表结构学习许多东西
- 基于map、reduce的hadoop
- 高阶表操作对分解程序复杂性很有意义
序对的操作
由于序对是构造复杂数据对象的基础,所有掌握序对的操作也就显得尤为重要,在学习这些操作时,我们可以感受到函数式编程的奇妙。 废话不多说,直接看代码list.scm看代码吧。
数据导向 vs. 消息传递
这两种方式是本章着重接受的两种数据抽象方式,分别对象函数式编程(数据导向)与面向对象编程(消息传递),具体辨析可参考习题2.76。
示例
由于本章大部分内容都是用具体例子来讲解,下面我就再一一回顾遍。大部分内容都在我Github的读书笔记中,这里相当于个索引,具体例子可参考给出的相应链接😊。
有理数运算
通过这里例子,引入数据抽象的意义。具体代码见rational.scm。
介绍完这个例子后,书上提出了一个重要的问题,“什么是数据”,在有理数运算这个例子,中我们能看到的就是一个构造函数make-rat,两个选择函数numer与demon。首先我们要明确,并不是任意三个过程都能构成有理数的实现,需要满足
(make-rat (numer x) (denom x)) = x
任意满足这一条件的三个函数,都能作为有理数表示的基础。 一般来说,一种数据对象的构造函数和选择函数都要满足一定条件。scheme中底层的数据结构序对也满足这一特点。
(car (cons a b)) = a
(cdr (cons a b)) = b
(cons (car x)(cdr x)) = x ;有前提,x 必须是序对
Church数
习题2.06引出Church数,完全用过程实现整数算术系统,关于这一点,推荐大家看我之前写的编程语言的基石——Lambda calculus,绝对能够颠覆你的思维。
区间运算
见相应的习题解答,推荐看习题2.14_2.16
八皇后问题
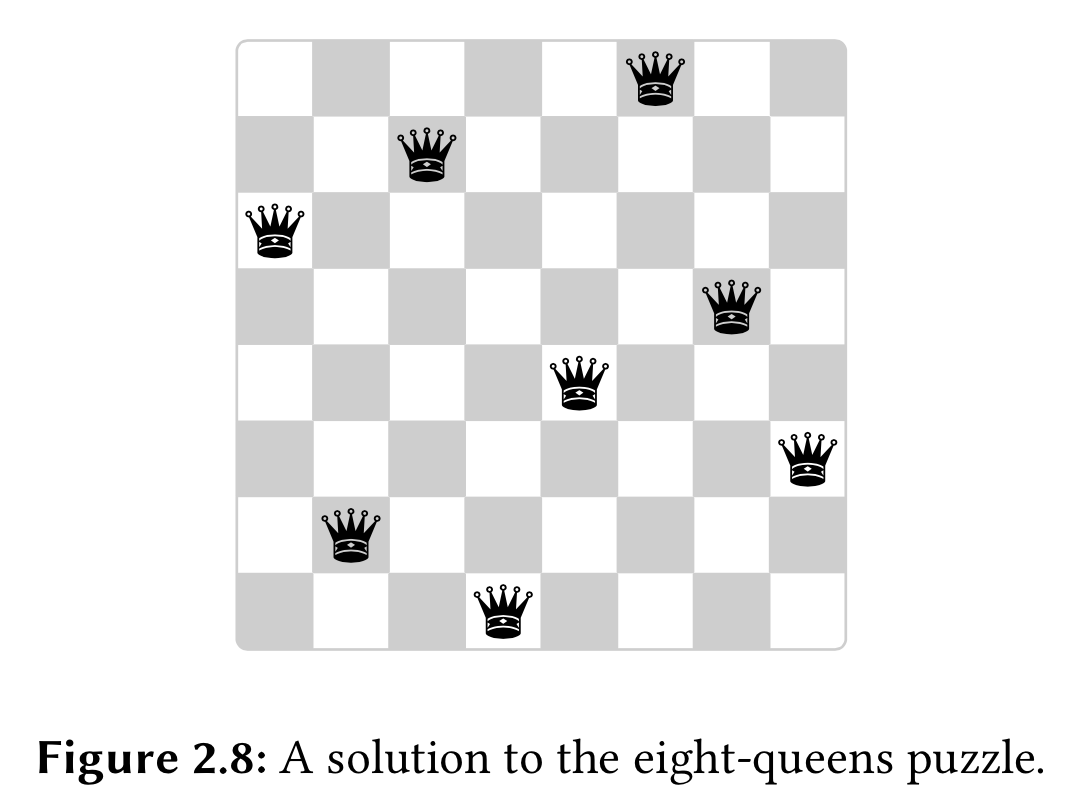
经典的问题,参考习题2.42。
图形语言

Huffman编码树🌲
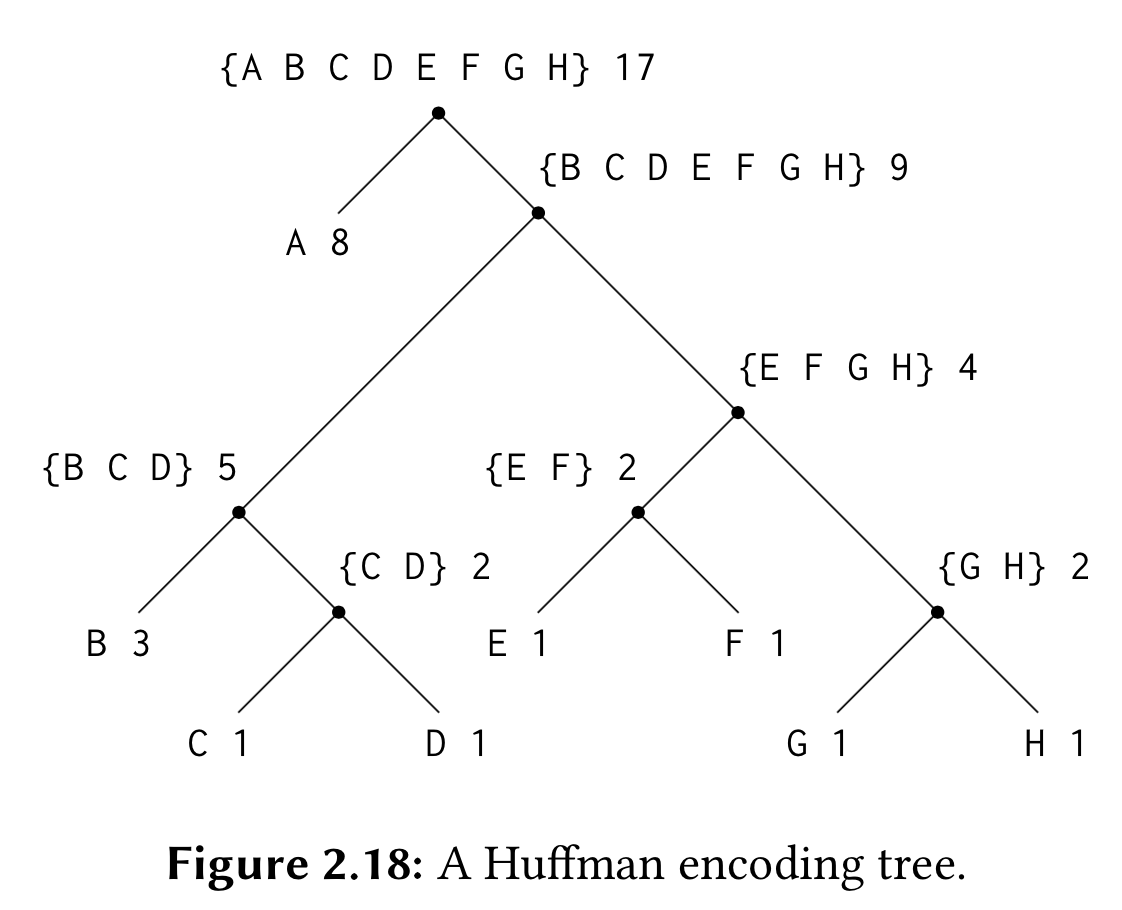
复数的表示
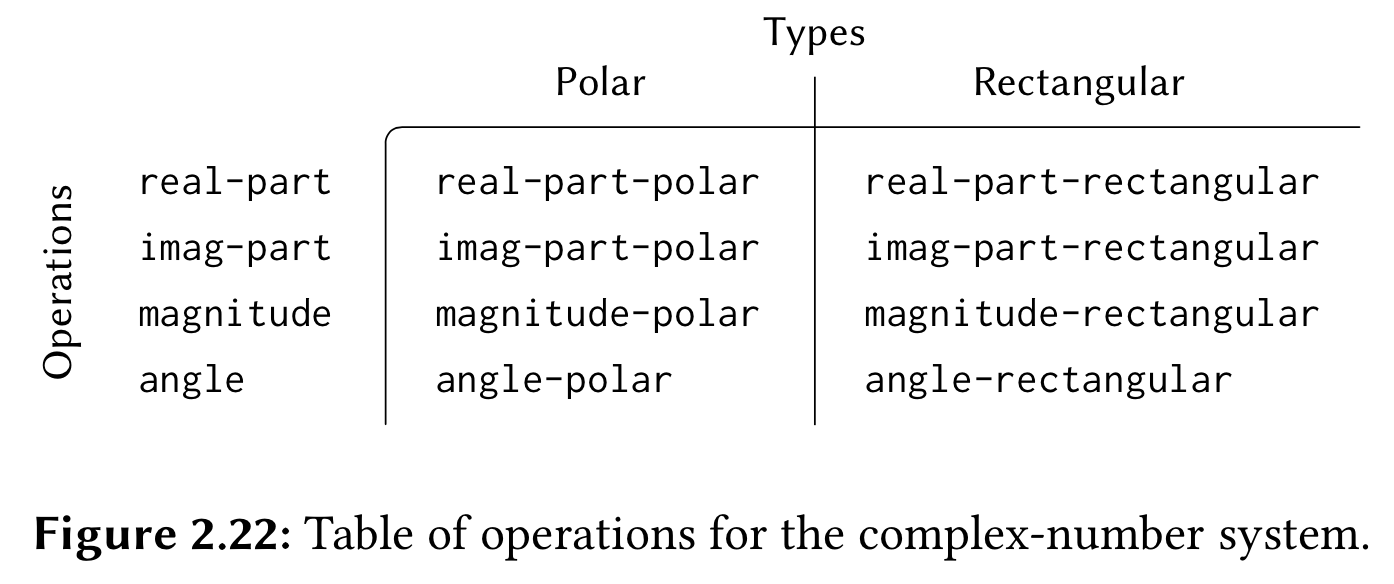
两种坐标的实现,参考代码lib/generic_arithmetic.scm
通用型算术包的实现
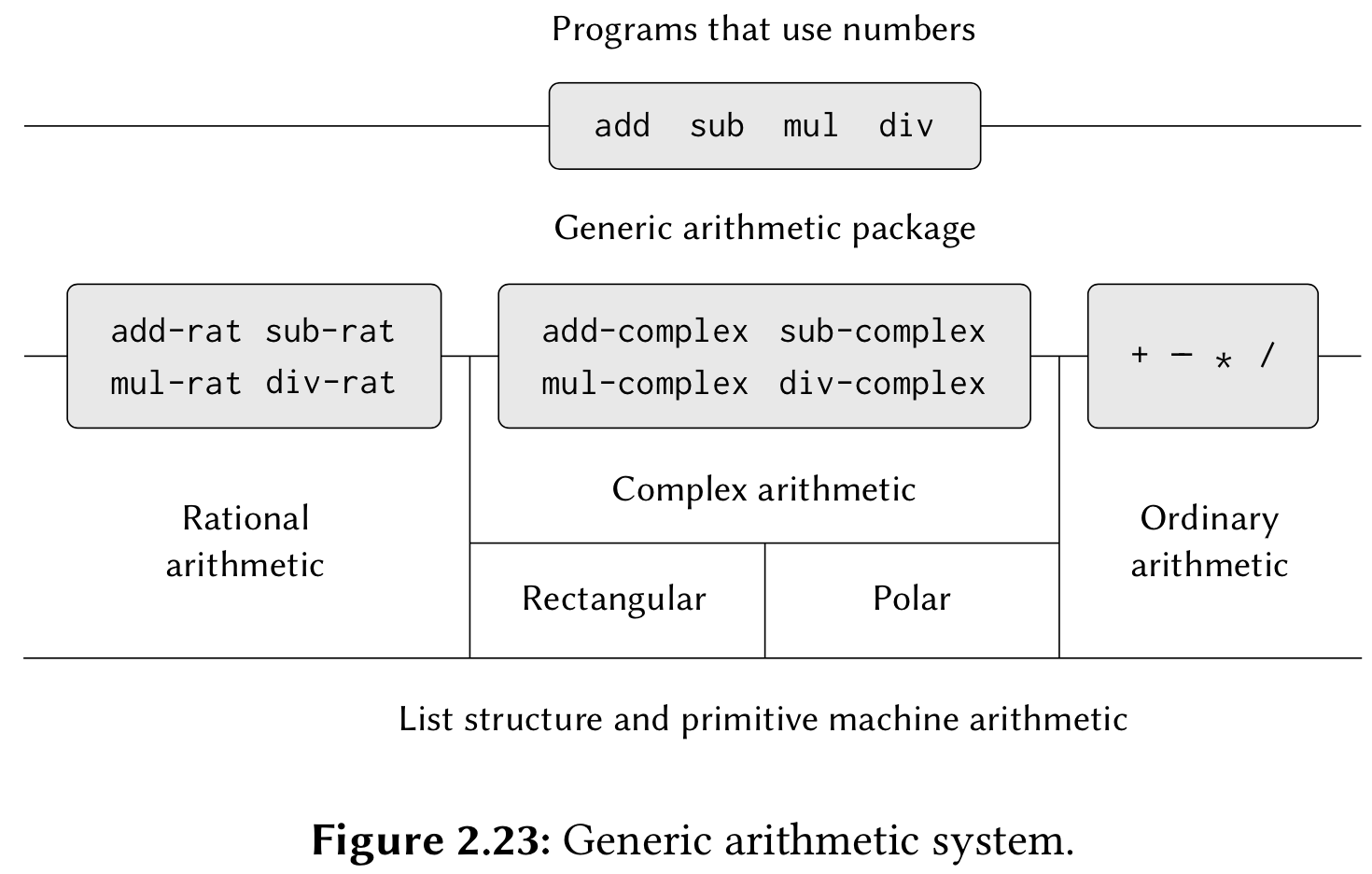
符号代数——多项式算术

从“强制”引出的问题可以看出强类型语言的劣势,现在像python、javascript等弱类型的语言这么火,很大程序上就是由于弱类型语言的编译器把“强制”的工作给做了,程序员根本不用去关心。当然,如果所有“强制”工作都让编译器去做,也是不合适的,具体如何选择,就需要综合多种因素了。 我本身经验还不是很丰富,就不乱说了,如果你有这方面的亲身体会,可以留言,我会及时更新😊。
代码实现参考lib/poly.scm与习题2.92。
扩充练习:有理函数
经过前面多项式算术的习题,我基本已经败下阵来了,实在是吸收消化不了了,改日再战😂。
总结
这一次看第二章,陆陆续续用了2个月,基本上耗费平时下班+周末双休的时间,收获还是挺大的。
不过由于本章习题量有些大,而且一开始像一些基础的过程put、get都没有,所以自己只是随便写写,没法运行,所以前面看的不好,这章习题之简的联系很紧密,前面没做好,后面只能呵呵了。
有一段时间让这些题弄的很烦,一点不想做,还好我这时候分散了下注意力,看了些其他的东西,像java集合框架的一些代码、the little schemer第九章的Y算子推导(虽然还没看懂),由于带着放松心情看的,遇到不懂的地方我就跳过去,没有深究,基本上达到了放松的目的。之后在网上把那些基础的过程都实现出来,再去做那些习题就顺多了。
这一章的内容,我之前多多少少了解过,所以大部分内容看起来还是比较顺畅的,就是习题多了点,由于当初给自己定的目标,所以还是慢慢的把所有习题(有理函数的除外)做了一遍。还是一点就是做后面的题时,忘了前面的知识点,需要平时没事多去翻翻,毕竟现在还达不到烂熟于心的地步。
下周一小组内再过一遍,向着第三章进军了。⛽️