SICP 第三章总结

历时三个月，终于把第三章看完了。这三月发生了太多的意外，本文不打算说了，后面在写 2015 年终总结时再来谈谈这三个月的事情。如今回过头来看看第三章的内容，好像也不怎么难，只是内容涉及的面稍微广一些而已，下面来回顾总结一下第三章。

主旨

第三章的标题为模块化、对象和状态，主要讨论与状态有关的编程问题。前面两章，讨论的问题主要是：

1. 如何组合基本过程和基本数据
2. 如何构造各种复合对象(组合过程/数据)
3. 抽象在控制和处理程序复杂性中的重要作用

但对于程序设计而言，上面这三种手段还不够用，有效设计大型系统，还需要一些组织系统的原则，这体现在下面两方面：

1. 只有一集高效算法，不足以构造出良好的大型系统
2. 系统的功能分解，结构组织和管理与算法一样重要(或更甚之)

为了系统化地完成设计，特别需要一些模块化策略。模块化就是把复杂系统分解为一些边界清晰、易于独立理解的部分；每个部分的内部成分之间关系较密切，内聚力强;不同部分具有良 好的功能分离，相互之间的交互清晰、容易认识和处理；良好模块化分解出的部分可以分别设计，分别开发和维护。

假设构造一个系统的目标是希望模拟一个真实世界的系统，一种有效策略就是基于被模拟系统的结构去设计程序的结构。这主要包括下面三个方面：

1. 针对实际物理系统中的每个对象，构造一个对应的程序对象
2. 针对实际系统里的每种活动，在计算系统里实现一种对应操作
3. 让所开发的系统的活动比较直接地反映被模拟系统的活动

采用这种设计系统策略，有一个重要问题必须考虑：

真实世界的系统是变化的（相应的，人的认识也不断深入）

这些变化在人工系统里的反映，通常是需要在系统里增加新对象或新操作，或者需要修改已有对象和操作的行为。

为了有效完成模拟，我们希望构造出的模拟系统在遇到变化时，做到下面两点：

1. 在修改时只需要局部做，不需要大范围改变程序
2. 在扩充时只需简单加入对象或操作，局部修改/加入相关操作

设计策略

本章针对上述目标，将讨论两种系统的组织策略：

1. 把系统看成是由一批相互作用的对象组成

   真实系统中的对象随着时间的进展不断变化，模拟它们的系统对象也吸引相应地变化

2. 把系统看作一种信号处理系统

   关注流过系统的信息流

基于对象的设计

基于对象，需要关注计算对象可以怎样变化而又同时保持其标识。这是一种新的计算模型，带来许多本质性变化，包括有关计算的基本观点，基本操作，抽象的计算模型及其实现。

赋值

为了说清楚让一个计算对象具有随时间变化状态，贯穿本章的例子是：银行账号。一个账号对于我们系统设计中的一个对象，对同一个对象调用同一方法，返回的结果缺不一致。例如，假设开始时账户有100元钱，在不断调用“取钱”过程时，得到结果是不一样的。

(withdraw 25)
75
(withdraw 25)
50
(withdraw 60)
"Insufficient funds"

这样的计算模型如果使用第一章介绍的替换计算模型，是不可能做到的，为此，本章引入了一新的计算模型，在该模型中，变量不在仅仅是某个值的名字，更准确的说，此时的变量标识了一个值的地址，这很像 C语言中的指针，面向对象中的值引用。

环境计算模型

(define (make-withdraw balance)
  (lambda (amount)
    (if (> amount balance)
      "Insufficient"
      (begin
        (set! balance (- balance amount))
        balance))))

(define W1 (make-withdraw 100))
(W1 50)

关于环境计算模型，核心点就两个：

1. 过程声明时，其外围指针指向其运行时的环境
2. 过程调用时，其外围指针指向声明时外围指针指向的那个环境

我自己尝试着用 Java 实现了一个 Scheme 方言，其中对这个环境模型也进行了模拟，大家不清楚的可以看看我这篇文章的介绍。

用变动的数据做模拟

在前两章中，没有赋值的概念，那时对于一种数据结构，我们只需明确其构造函数与选择函数即可使用该数据结构，在之前两章中，我们介绍了“表”、“树”这两种数据结构，引入了赋值后，一个数据结构多了一种函数，即修改函数，利用修改函数，3.3 小节介绍了“变动的表”、“队列”、“表格”三种新的数据结构。

变动的表

变动的表这一数据结构，主要是借助set!，实现了set-car!与set-cdr!，进而可以实现变动的表，其中比较有意思的是习题3.19，让我们在O(1)空间复杂度检查一个表中是否包含环，这也是面试题中经常出现的一道，大家一定要掌握。基本思路就是

设置两个指针，一个一次走一步，另一个一次走两步，然后如果两个指针相等，那么就说明有环存在。

更进一步，如果一个表中有环的存在，如何找出那个环的交叉点（即如何找出下图中的m点）。如果不清楚，可以参考我习题3.19 的解答。

队列

队列是一个“先进先出”的数据结构，这里主要是引入首尾指针的思想来加速对队列末端的访问。队列的实现可以参考我 Github 库的/exercises/03/lib/queue.scm。 其中习题3.23让我们实现一双向链表，一种很实用的队列的变种，大家一定要自己做一下。

表格

这里的表格和我们Java中的Map、Python中的dict类型比较类似。

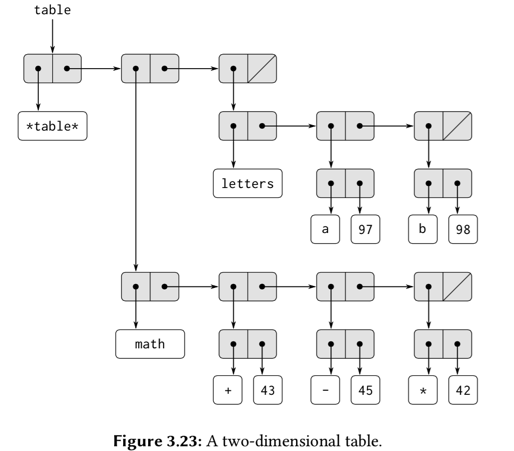
其中比较有意思对是习题3.25，让我们推广一维表格、二维表格的概念，实现任意多个关键码的表格，比较有趣。

数字电路的模拟器

这是本章一个比较实际的例子，其背景是

数字系统（像计算机）都是通过连接一些简单元件构造起来的，这些元件单独看起来功能都很简单，它们连接起来形成的网络就可能产生非常复杂的行为。

从上面这个半加器可以看出

由于各个门部件延迟的存在，使得输出可能在不同的时间产生，有关数字电路的设计的许多困难都源于此。

这里的模拟器主要包含下面两部分：

1. 构造电路的基本构件，像反门、与门、或门
2. 传递数字信号的连线

除了上面两部分，为了模拟门部件延时的效果，本系统引入待处理表。这三部分都是用Scheme的过程实现，用内部状态表示该对象的改变，具体代码可以参考simulator.scm。

其中比较有意思的是习题3.31，大家可以好好想想。

(define (accept-action-procedure! proc)
  (set! action-procedures (cons proc action-procedures))
  ; 这里将 proc 加入后，立即执行了 proc，为什么？ 见习题3.31
  (proc))

约束的传播

本章另一个比较实用的例子，之前我们的过程都是单向，我们只能通过一个过程的输入获得其输出，但是这里给我们展示了如何构建一个约束系统，是的我们可以从任意方向求过程的未知数的值。

在讲解这个实例时，3.3.5小节引入一新语言的设计，这种语言将使我们可以基于各种关系进行工作。

我们在第一章里面就知道了，任何一门语言都必须提供三种机制：基本表达形式、组合的方法与抽象的方法。针对本系统的语言的基本元素就是各种基本约束，像adder、multiplier、constant。用 Scheme 过程来实现基本约束也就自动地为该新语言提供了一种复合对象的抽象方式。

整个约束系统，我个人觉得主要是理解process-forget-value过程中为什么要调用process-new-value，这是串联起整个约束系统很重要的一步。书上是这么解释的：

只所以需要这一步，是因为还可能有些连接器仍然有自己的值（也就是说，某个连接器过去所拥有的值原来就不是由当前对象设置的）

; adder 中 process-forget-value 的实现
(define (process-forget-value)
  (forget-value! sum me)
  (forget-value! a1 me)
  (forget-value! a2 me)
  ; TODO 为什么需要理解执行 process-new-value
  (process-new-value))

整个约束系统的代码可以在propagation.scm找到。

并发，时间是一个本质问题

这一小节主要讲解引入赋值这一行为后，并发程序可能出现的问题，其实这里的东西我们在平常的编程中多多少少有些了解，主要是如何保证操作的原子性。

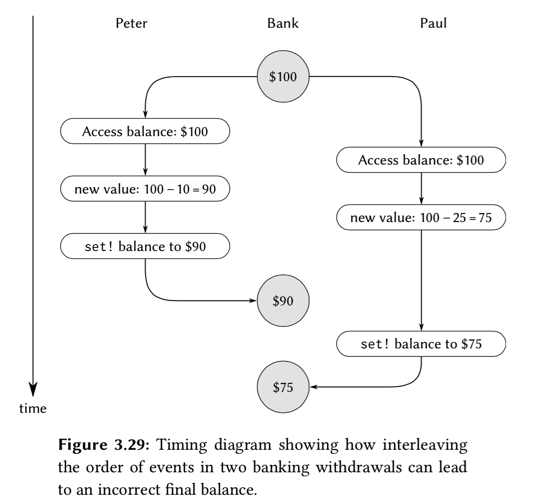
更进一步，如果保证 n 对象间交互的原子性呢？这应该就是现在比较热门的一领域：分布式系统中，如何保证数据的一致性，后面有精力可以看看看业界使用最广泛的 zookeeper 的实现原理。

书上进一步扩展，讲述了并发问题与物理学的联系。有种发现一世界未解之谜的感觉，摘抄如下：

从本质上看，在并发控制中，任何时间概念都必然与通信有内在的密切联系。有意思的是，时间与通信之间的这种联系也出现在相对论里，在那里的光速（可能用于同步事件的最快信号）是与时间和空间有关的基本常量。在处理时间和状态时，我们在计算模型领域所遭遇的复杂性，事实上，可能就是物理世界中最基本的复杂性的一种反映。

流

流是另一种模拟现实物理世界的设计策略，其核心思想就是用数学概念上的函数来表示一现实物体的改变，比如对象X，可以用X(t)来表示，如果我们想集中关心的是一个个时刻的x，那么就可以将它看作一个变化的量。如果关注的是这些值的整个时间史，那么就不需要强调其中的变化——这一函数本身是没有改变的。

这里流，较之前的表而言，主要是引入force、delay两个过程，将其延时求值。有了延时求值，我们就可以做很多之前不能做的事情，比如实现一个表示所有正整数的无穷流

; 第一种方式
(define (integers-starting-from n)
  (cons-stream n (integers-starting-from (+ n 1))))
(define integers (integers-starting-from 1))
; 第二种方式，隐式定义
(define ones (cons-stream 1 ones))
(define (add-streams s1 s2)
  (stream-map + s1 s2))
(define integers2 (cons-stream 1 (add-streams ones integers2)))

流计算模式的使用

流方法极富有启发性，因为借助于它去构造系统时，所用的模块划分方式可以与采用赋值，围绕着状态变量组织系统的方式不同。例如，我们可以将整个的时间序列作为有关的目标，而不是去关注状态变量在各个时刻的值。这将使我们更方便地组合与比较来自不同时刻的状态的组合。

将迭代操作表示为流操作

; 求解一个数的平方
(define (sqrt-stream x)
  (define guesses
    (cons-stream 1.0
                 (stream-map (lambda (guess) (sqrt-improve guess x))
                             guesses)))
  guesses)
; 由 π/4 = 1- 1/3 + 1/5 - 1/7 + ..... 计算 π 的值
(define (pi-summands n)
  (cons-stream (/ 1.0 n)
               (stream-map - (pi-summands (+ n 2)))))
(define (partial-sums s)
  (cons-stream (stream-car s)
               (add-streams (stream-cdr s)
                            (partial-sums s))))
(define pi-stream
  (scale-stream (partial-sums (pi-summands 1)) 4))

序对的无穷流

将流作为信号

流的弊端

总结

本章一开始就提出了其目标，那就是构造一些计算模型，使其结构能够符合我们对于试图去模拟的真实世界的看法。我们学到了两种方式：

1. 将这一世界模拟为一集相互分离的、受时间约束的、具有状态的相互交流的对象
2. 将它模拟为单一的、无时间也无状态的统一体

每种方式都具有强有力的优势，但就其自身而言，有没有一种方式能够完全令人满意。如何整合这两个系统，是现在一重要难题。