深入浅出垃圾回收（二）Mark-Sweep 详析及其优化

发布: 2018-07-08   上次更新: 2024-11-02   分类: 理解计算机   标签: GC

文章目录

在上一篇文中介绍的追踪类（tracing）GC 较引用计数（Reference Counting）性能更高，但原生的追踪类 GC 也有其自身缺点，需要对其进行改造才能真正的名副其实。这篇文章就来介绍与之相关的内容。

术语

为了后面叙述方便，首先明确以下几个名词的含义：

MS 基本流程

首先来回顾下追踪类 GC 最基本的 mark-and-sweep 算法 ：先扫描整个 heap，标出可到达对象，然后执行 sweep 操作回收不可到达对象。这个算法本身比较简单，下面给出其实现伪代码：

// mutator 通过 new 函数来申请内存
new():
    ref = allocate()
    if ref == null
        collect()
        ref = allocate()
        
        if ref == null
            error "Out of memory"
    return ref

atomic collect():  // 这里 atomic 表明 gc 是原子性的，mutator 需要暂停
    markFromRoots()
    sweep(heapStart, heapEnd)
    
markFromRoots():
    initialize(worklist)
    
    for each reference in Roots  // Roots 表示所有根对象，比如全局对象，stack 中的对象
        if ref != null && !isMarked(reference)
            setMarked(reference)
            add(worklist, reference)
            mark()          // mark 也可以放在循环外面
            
            
initialize():
    // 对于单线程的collector 来说，可以用队列实现 worklist
    worklist = emptyQueue()

//如果 worklist 是队列，那么 mark 采用的是 BFS（广度优先搜索）方式来遍历引用树                
mark():
    while !isEmpty(worklist):
        ref = remove(worklist)  // 从 worklist 中取出第一个元素
        for each field in Pointers(ref)  // Pointers(obj) 返回一个object的所有属性，可能是数据，对象，指向其他对象的指针
            child = *field
            if child != null && !isMarked(child)
                setMarked(child)
                add(worklist, child)
                
sweep(start, end):
    scan = start
    while scan < end
        if isMarked(scan)
            unsetMarked(scan)
        else
            free(scan)
        scan = nextObject(scan)

通过上面伪代码描述，不难得出 MS 有以下问题：

  1. heap 容易出现碎片
  2. 破坏引用本地性（由于对象不会被移动，存活的对象与空闲空间交错在一起）
  3. GC 时间与 heap 空间大小成正比
  4. 在进行 GC 期间，整个系统会被挂起，即stop-the-world

需要说明一点，RC 类 GC 同样有前两个问题，但是对于 RC 来说，并没有好的优化措施来缓解。下面我们就来看追踪类 GC 是如何解决上述问题。

优化MS

Bitmap marking

在 mark 过程中，需要去标记（mark-bits）对象的 liveness，有两种方式来实现：

  1. 在每个对象的header部分（in-object mark-bit）
  2. 使用一个单独的 bitmap，每一位 bit 对应一个对象

两种方式各有利弊，需要结合具体场景进行分析。In-object mark-bit 是最直接的方式，对于 JVM/.NET 运行时来说，每个 object 都会有 header，使用这种方式也就理所应当了； 对于 bitmap 来说，需要在 bit 位与 object 之间进行映射，这就要求 object 进行对齐，比如：heap 大小为 65536 字节，所有的对象以 16 字节对齐，那么堆内就有 4096 个地址可以作为对象的起始地址，与之对应需要 4096 个 bit 即 512 个字节。除此之外，bitmap 还有下面两个优势：

  1. sweep 操作更高效，这是由于 bitmap 结构紧凑，可以一次性加载到内存中；通过整型的 ALU 操作与条件分支（conditional branch） 一次性可进行 32 位的检测
  2. 在类 Unix 系统中，bitmap 有利于 fork() 出来的进程与主进程进行 copy-on-write 数据共享，Ruby 2.0 就因此获得较大性能提升。

下面给出 bitmap 方式的伪代码：

mark():
    cur = nextInBitmap()
    while cur < heapEnd
        add(worklist, cur)
        markStep(cur)
        cur = nextInBitmap()
        
markStep(start):
    while !isEmpty():
        ref = remove(worklist)
        for each field in Pointers(ref):
            child = *field
            if child != null && !isMarked(child)
                setMarked(child)
                if child > start         //这里与之前不同，只需要把高于当前地址的子节点加入到 worklist 即可
                    add(worklist, child)

Lazy sweeping

MS 算法有以下几个特点：

  1. 某对象一旦被标为garbage，它永远都会是 garbage，不会被 mutator 再访问
  2. mutator 不能修改 mark-bit

基于以上几点，sweep 操作完全可以与 mutator 同时运行（parallel）的。 Lazy sweep 指的是把较为耗时（相对 mark 来说）的 sweep 操作放在 allocate 过程中，并且只在有足够的空间时才去真正进行回收。Ruby 1.9.3 引入 lazy sweep 获得较大性能提升。

atomic collect():
    markFromRoots()
    for each block in Blocks  // 这里以 block 为单位管理更高效
        if not isMarked(block)
            add(blockAllocator, block)
        else
            add(reclaimList, block)    // 把待回收的 block 放入队列中延迟回收
            
atomic allocate(sz):
    result = remove(sz)
    if result = null
        lazySweep(sz)
        result = remove(sz)
    return result
    
lazySweep(sz):
    repeat
        block = nextBlock(reclaimList, sz)  // 这里需要分配一个 sz 大小的 block，可见 block 需要按大小 group 起来管理
        if block != null
            sweep(start(block), end(block))
            if spaceFound(block)
                return
    until block == null
    allocSlow(sz)
    
allocSlow(sz):
    block = allocateBlock(sz)
    if block != null
        init(block)

Lazy Sweep 除了降低 sweep 阶段 mutator 的暂停时间外，还有以下优点：

其他优化

除了上面介绍的两类优化，比较新的优化手段还有如下几个：

鉴于篇幅原因，这里不再讲述，感兴趣的读者可自行搜索。

碎片问题

上面优化的措施虽然能提高 MS 性能，但都无法解决 heap 碎片问题，这就需要新的算法去解决。

Mark-Compact

MC 算法与 MS 类似，先是一个 mark 过程标记可到达对象，这里取代 sweep 的是一个 compact，工作流程如下：

  1. 重新安排（relocate）可到达对象
  2. 更新指向可到达对象的指针

关于第一步中的安排策略，一般有如下三种选择：

  1. 任意（Arbitrary）。特点是快，但是空间的 locality 较差
  2. 线性（Linearising）。重新分配到附近有关系的（siblings/pointer/reference…）对象周边
  3. 滑动（Sliding）。所有活对象被滑动到 heap 的一端，保证原有顺序，这有利于改善 locality 的情况。这是现在采用较多的方案

对于采用 MC 的系统，allocate 过程就变得较为简单，只需要bump pointer 即可。 但是这类算法需要多次遍历对象，第一次遍历算出对象将要移动到的新位置，接下来的遍历来真正移动对象，并更新指针，所以MC相对MS要更耗时，这在 heap 较大时更为明显。 这里比较有名的是 Edward 的 Two-pointer 压缩算法。大致过程如下：

  1. 在 heap 两端各准备一指针，由外向内 scan 寻找可压缩的对象
  2. 自顶向下的指针寻找可到达对象，自底向上的指针寻找 heap 中的“洞”来存放可到达对象

关于这个算法还有很多变种，这里不在讲述，感兴趣可以自行搜索：

Copying GC

MC 算法虽然能解决内存碎片问题，但是需要多次遍历heap空间，这会导致较大性能损耗，Copying GC 采用空间换时间的方式来提升性能。 这类 GC 并不会真正去“回收”不可到达对象，而是会把所有可到达对象移动到一个区域，heap 中剩余的空间就是可用的了（因为这里面都是垃圾）。这里并没有进行 sweep/compact，而是用 scavenging（净化） 来描述回收这一过程。

Semispace collector

Copying GC 典型的代表半空间回收器（semispace collector）。其工作过程是这样的：

  1. heap 被分成2份相邻的空间（semispace）：fromspace 与 tospace
  2. 在程序运行时，只有 fromspace 会被使用（分配新对象）
  3. 在 fromspace 没有足够空间容纳新对象时，程序会被挂起，然后把 fromspace 的可到达对象拷贝到 tospace
  4. 在拷贝完成时，之前的2个空间交换身份，tospace 成了新一轮的 fromspace

semispace 示意图
semispace 示意图

Cheney 算法

Cheney 算法是用来解决如何遍历引用关系图，将之移动到 tospace 的算法，其步骤如下：

  1. 所有可直接到达的对象组成一队列，作为宽度优先遍历的起点，同时有两个辅助指针：scan 指针指向起始位置，free 指针指向末尾
  2. 通过移动 scan 来依次遍历队列，当 scan 的对象存在指向 fromspace 中对象的指针时，把被指向的对象添加到队列末端，同时更新指针，使之指向新对象；
  3. 更新 free 使之始终指向队列末尾，重复步骤2
  4. 当 scan 移动到队列末尾时，算法结束

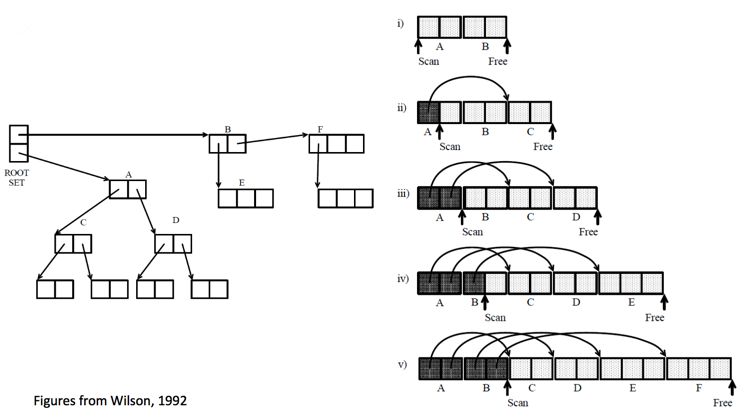
Cheney 宽度优先遍历复制示意图
Cheney 宽度优先遍历复制示意图

如果按照上述算法操作，会把被指向多次的对象复制多次，所以在拷贝对象到 tospace 时，会在原始版本的对象上记录一个重定向指针（forwarding pointer），来标明这个对象已经被复制过了，并且告知新对象的位置；后面 scan 对象时，如果发现具有重定向指针的对象时就会跳过复制操作，直接更新指针就可以了。

initialize():
    tospace = N/2
    fromspace = 0
    allocPtr = fromspace
    scanPtr = whatever // 只在 collect 阶段使用
    
allocate(n):
    if allocPtr + n > fromspace + N/2
        collect()
    if allocPtr + n > fromspace + N/2
        fail "Insufficient memory"
    
    o = allocPtr
    allocPtr = allocPtr + n
    return o
    
atomic collect():
    swap(fromspace, tospace)
    allocPtr = fromspace
    scanPtr = fromspace
    
    for each field in Roots
        copy(field)
        
    while scanPtr < allocPtr:
        for each reference in o // scanPtr 指向 o
            copy(reference)
        scanPtr = scanPtr + o.size()

copy(o):
    if hasForwardingAddress(o)
        return forwardAddress(o)
    else
        o' = allocPtr
        allocPtr = allocPtr + o.size()
        copy the contents of o to o'
        forwardAddress(o) = o'

优缺点

通过上述描述，不难发现Copying GC 一最大缺点在于所需空间翻倍，不过现如今内存已经普遍较大，这个问题不是很严重。 其次，复制的效率于可到达对象成正比，如果每次 GC 时可到达对象相近，那么降低 GC 频率就会减少 GC 对程序的影响。如果降低 GC 频率呢？答案就是加大 semispace 空间，这样程序就需要更多的时间来填满它。

如果程序中有一些大对象体积（比如：大数组），且存活时间较长，那么这个复制操作对程序影响就会会比较严重，基于此，Baker 提出了一种衍化方案：Non-Copying Implicit GC

Non-Copying Implicit GC

这类 GC 从 Copying GC 衍化而来，巧妙之处在于，semispace 不必是物理上分割的空间，可以用两个用双向链表来表示，一般称为 ：from-set 与 to-set。为了实现这种策略，需要在每个对象上多加以下两个信息：

当 from-set 耗尽时，只需遍历 from-set，把其中的可到达对象插入到 to-set，然后改变flag即可，复制操作变成了链表指针操作。这类 GC 的优势除了不用进行真正的拷贝外，还有下面两处优点：

  1. 语言级别的指针不需要改变了（因为对象没动），这对编译器的要求更小了
  2. 如果一个对象不含有指针，那么就没必要 scan 了

缺点当然也比较明显：

所以这类 GC 虽然是 Copying GC 的优化，但也只适用于某些特定的场景。

总结

通过上面的介绍，觉得最重要的就是要分清一个算法的优势与劣势，软件工程里面没有「银弹」，都是有取舍的。 上面对 MS 算法的优化，基本都是在 sweep 阶段，mark 阶段没怎么改进。鉴于文章篇幅，将在下一篇中介绍 Incremental GC，来说明如何优化 mark 阶段；而且通过不断研究，前辈们总结出「大部分对象的生命周期较短」的特性，所以就延伸出了 Generational GC，这也将在下文中介绍。Stay Tuned！

参考

评论

欢迎读者通过邮件与我交流，也可以在 Mastodon 或 Twitter 上关注我。